Circle-circle intersection and more

**prometheuzz** · May 11 '07, 09:19 AM

Originally posted by okan

Hi everyone,

I have a java method public static String circleRelation( double x1, double y1, double r1, double x2, double y2, double r2) that - given two circles in the plane - will decide whether those circles (1) encircle each other, (2) intersect, (3) touch or (4) are totally seperate. The method returns a String which describes the relationship between those circles, e.g.:
The first circle encircles the second circle
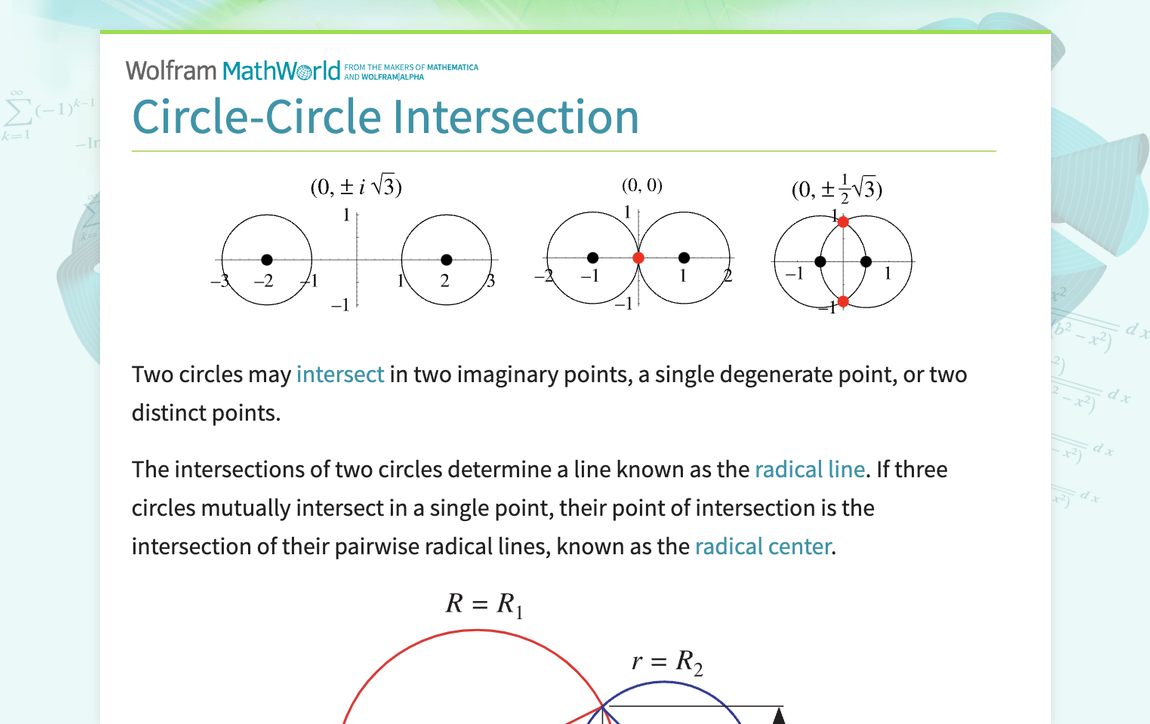
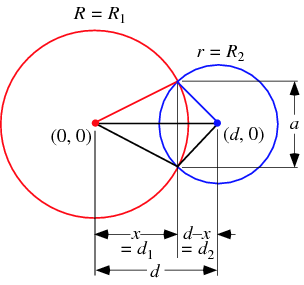
The circles intersect
The circles touch each other
The circles are seperate

Do you have any sample codes to write especially about circles intersect?

I once wrote such a thing and used this page as a reference:

Circle-Circle Intersection -- from Wolfram MathWorld

http://mathworld.wolfram.com/Circle-CircleIntersection.html

Two circles may intersect in two imaginary points, a single degenerate point, or two distinct points. The intersections of two circles determine a line known as the radical line. If three circles mutually intersect in a single point, their point of intersection is the intersection of their pairwise radical lines, known as the radical center. Let two circles of radii R and r and centered at (0,0) and (d,0) intersect in a region shaped like an asymmetric lens. The equations of the two...

Checkout reply #10 from this thread:
<Link removed by Admin: Linking to other forums is against site rules>
where I gave an example of how to create such a method.

Good luck.

**prometheuzz** · May 12 '07, 11:58 AM

Originally posted by prometheuzz

...
<Link removed by Admin: Linking to other forums is against site rules>
...

OK, then I'll cross post my answer.

Let's say you're trying to find the intersection points of the circles C1 and C2 where C1 has it's center point at (-9, 1) and has a radius of 7, and C2's center lies at (5, -5) and has a radius of 18.
Note that I posted the image to make clear what the variables names in the formula's are.

First calculate the distance, 'd', between the center-points of the two circles:

Code:

d = √(|-9 - 5| + |1 - -5|)
  = 15.23

Now we calculate 'd1':

Code:

d1 = (r1^2 - r2^2 + d^2) / 2*d
   = (7^2 - 18^2 + 15.23^2) / 2*15.23
   = (49 - 324 + 231.95) / 30.46
   = -43.05 / 30.46
   = -1.41

Now we solve 'h', which is 1/2 * 'a'

Code:

h = √(r1^2 - a^2)
  = √(7^2 - -1.41^2)
  = √(49 - 1.99)
  = 6.86

To find point P3(x3,y3) which is the intersection of line 'd' and 'a' we use the following formula:

Code:

x3 = x1 + (d1 * (x2 - x1)) / d
   = -9 + (-1.41 * (5 - -9)) / 15.23
   = -10.29
y3 = y1 + (d1 * (y2 - y1)) / d
   = 1 + (-1.41 * (-5 - 1)) / 15.23
   = 1.55

Last but not least, calculate the points P4_i and P4_ii which are the intersection points of the two circles:

Code:

x4_i = x3 + (h * (y2 - y1)) / d
     = -10.29 + (6.86 * (-5 - 1)) / 15.23
     = -12.99
y4_i = y3 - (h * (x2 - x1)) / d
     = 1.55 - (6.86 * (5 - -9)) / 15.23
     = -4.75

x4_ii = x3 - (h * (y2 - y1)) / d
      = -10.29 - (6.86 * (-5 - 1)) / 15.23
      = -7.59
y4_ii = y3 + (h * (x2 - x1)) / d
      = 1.55 + (6.86 * (5 - -9)) / 15.23
      = 7.86

So, as you can see, the intersection points are (-12.99, -4.75) and (-7.59, 7.86).

**AnonymousXXX** · Nov 11 '13, 05:36 PM

there is java code to do this:

GitHub - Lanchon/circle-circle-intersection: Circle-to-Circle Intersections in Java

https://github.com/Lanchon/circle-circle-intersection

Circle-to-Circle Intersections in Java. Contribute to Lanchon/circle-circle-intersection development by creating an account on GitHub.

Circle-circle intersection and more

Circle-circle intersection and more

Comment

Comment

Comment