Falsification of probability
exploring possibility of falsification of random
qbasic qb64 programs were created in an hour
and a table using formulas
= CASEBETWEEN(0;1 )
= IF (B3 = B2; C2 + 1; 0)
= COUNTIF (C$3: C$55000; D2)
= SUM(E2:E10)
= E2 / E3
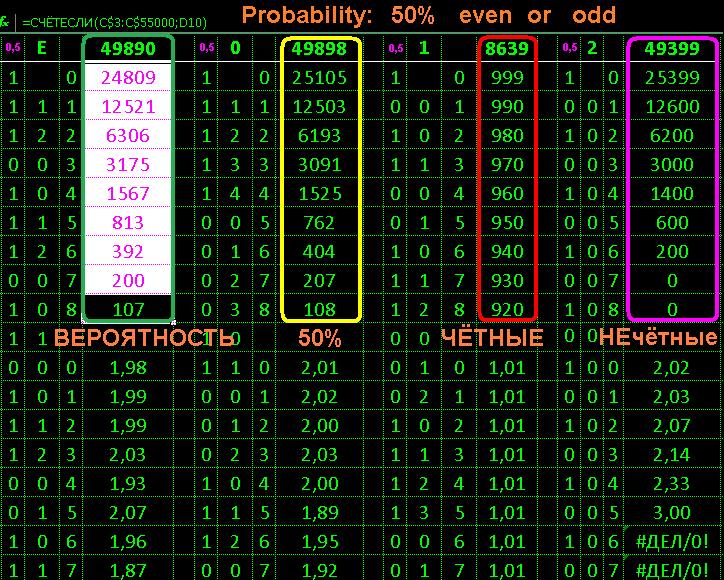
idea: fake a 50% chance
results:
research E green pure excel:
randomly distributed naturally
research 0 yellow qb 0:
randomly distributed naturally
research 1 in red qb 1:
explicit fake equal number in a row
research 2 violet qb 2:
smart fake but not all programmed
and skew due to algorithm
Conclusion: identify fake random real
sequence fake shuffled
turns into a random sequence
and began to correspond to distributions
and excel more clearly than programs
but c# synthesis programs are possible online
using a random synthesis program
and dividing into small 0 and large 1
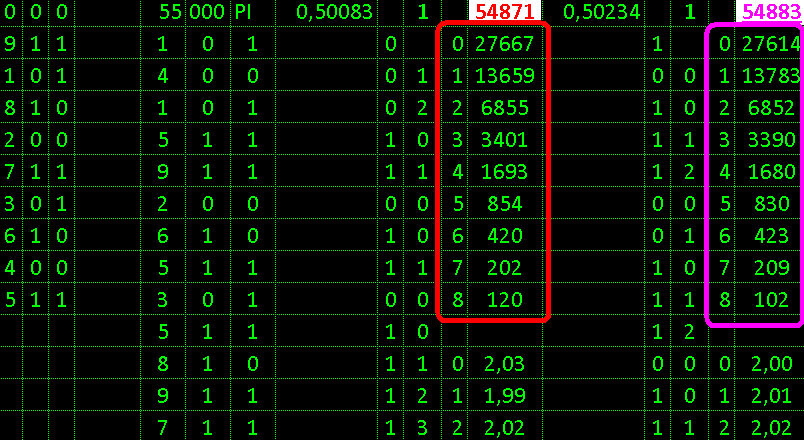
synthesized 55000 random and tested
despite normality of number of consecutive 0...7
a larger number in a row is not possible
therefore sequence is worse than usual rnd
in C# randomness is also low-power
I suppose understood by people as supposedly normal
on-line compiler: https://rextester.com/WXH62544
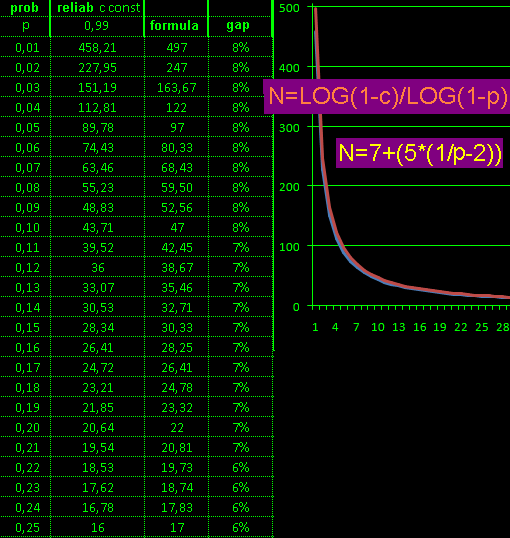
significant reliable probability: shuffled
that is: 2-sided and that is: integraly probability
Program peretas.bas creates a sequence
random a: 0 and 1 by manual algorithm from Internet
and program creates random d: 0 ... 77777
for shuffling and sorting an array d array a is ordered
and perhaps against repetition it is better to shuffle cards 1000000
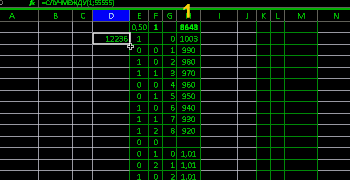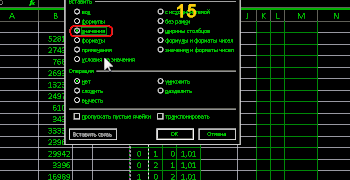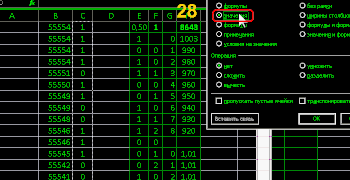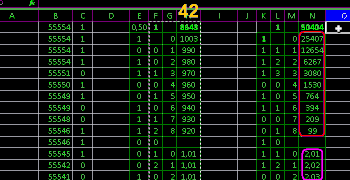
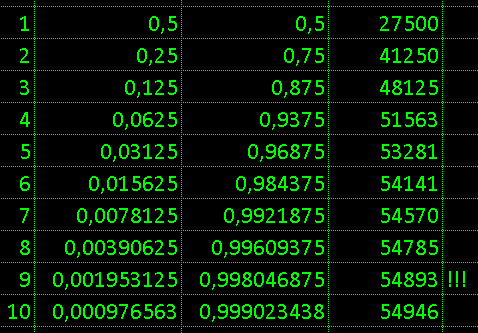
Theoretical values in Excel Excel via formulas
=C3/2
=D3+C4
=D4*55000
show: out of 55000 for 7 steps covered 54570
numbers in their sequences
and probably deviation betrays a false accident
and shuffling involved 54885 close to theory
Theoretical values in Excel Excel via formulas
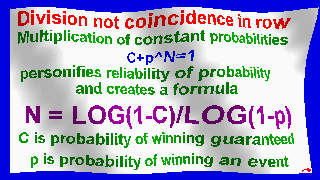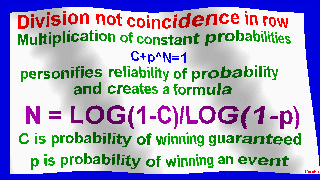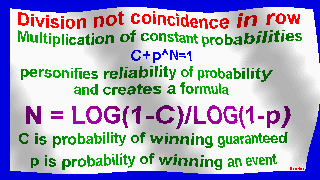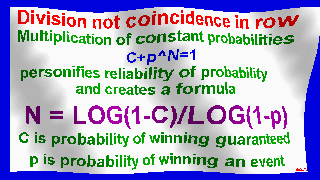
exploring possibility of falsification of random
qbasic qb64 programs were created in an hour
and a table using formulas
= CASEBETWEEN(0;1 )
= IF (B3 = B2; C2 + 1; 0)
= COUNTIF (C$3: C$55000; D2)
= SUM(E2:E10)
= E2 / E3

idea: fake a 50% chance
results:
research E green pure excel:
randomly distributed naturally
research 0 yellow qb 0:
randomly distributed naturally
research 1 in red qb 1:
explicit fake equal number in a row
research 2 violet qb 2:
smart fake but not all programmed
and skew due to algorithm
Conclusion: identify fake random real
Code:
' 0.bas OPEN "0.txt" FOR OUTPUT AS #1 FOR s = 1 TO 50000: PRINT #1, (INT(RND * 1000) MOD 2): NEXT CLOSE
Code:
' 1.bas OPEN "1.txt" FOR OUTPUT AS #1 FOR d = 1 TO 5: FOR s = 1 TO 100 FOR i = 1 TO s: PRINT #1, 1: NEXT FOR i = 1 TO s: PRINT #1, 0: NEXT NEXT: NEXT: CLOSE
Code:
' 2.bas OPEN "2.txt" FOR OUTPUT AS #1 FOR k = 1 TO 100: FOR s = 1 TO 7 FOR d = 1 TO 2 ^ (7 - s) FOR i = 1 TO s: PRINT #1, 1: NEXT FOR i = 1 TO s: PRINT #1, 0: NEXT NEXT: NEXT: NEXT: CLOSE
turns into a random sequence
and began to correspond to distributions

and excel more clearly than programs
but c# synthesis programs are possible online
using a random synthesis program
and dividing into small 0 and large 1
synthesized 55000 random and tested
despite normality of number of consecutive 0...7
a larger number in a row is not possible
therefore sequence is worse than usual rnd
Code:
'rndxx.bas
OPEN "rndxxx.txt" FOR OUTPUT AS #1
FOR i = 1 TO 55555: r = Rand
IF r < 0.5 THEN PRINT #1, 0 ELSE PRINT #1, 1
'IF r <= 0.5 THEN PRINT #1, 0 ELSE PRINT #1, 1
'IF r <= 0.7 THEN PRINT #1, 0 ELSE PRINT #1, 1
NEXT: CLOSE
FUNCTION Rand: STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1: Rand = x1 / 2 ^ 24
END FUNCTION

in C# randomness is also low-power
I suppose understood by people as supposedly normal
Code:
using System;using System.Linq;
using System.Collections.Generic;
using System.Text.RegularExpressions;
namespace Rextester
{ public class Program
{ public static void Main(string[] args)
{ Random rand = new Random();
for (int i = 1; i < 5555; i++)
{ var d = rand.Next(2);
if (d<0.5)
Console.WriteLine("0");
else Console.WriteLine("1");
}}}}
significant reliable probability: shuffled
that is: 2-sided and that is: integraly probability
Program peretas.bas creates a sequence
random a: 0 and 1 by manual algorithm from Internet
and program creates random d: 0 ... 77777
for shuffling and sorting an array d array a is ordered
and perhaps against repetition it is better to shuffle cards 1000000
Code:
'peretas.bas
DIM a(55555), d(55555)
OPEN "aa.txt" FOR OUTPUT AS #1: OPEN "dd.txt" FOR OUTPUT AS #2
OPEN "aaaa.txt" FOR OUTPUT AS #3: OPEN "dddd.txt" FOR OUTPUT AS #4
FOR i = 1 TO 55555: r = Rand: a(i) = INT(r * 2): PRINT #1, a(i): NEXT
FOR i = 1 TO 55555: r = Rand: d(i) = INT(r * 77777): PRINT #2, d(i): NEXT
FOR i = 1 TO 55554: FOR j = i TO 55555
IF d(i) > d(j) THEN SWAP d(i), d(j): SWAP a(i), a(j)
NEXT: NEXT
FOR i = 1 TO 55555: PRINT #3, a(i): PRINT #4, d(i): NEXT
CLOSE
FUNCTION Rand
STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1
Rand = x1 / 2 ^ 24
END FUNCTION
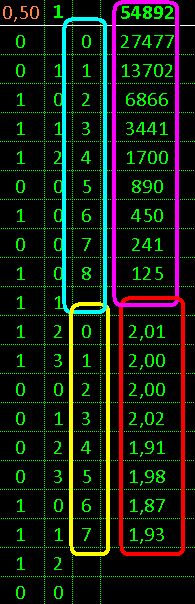
Theoretical values in Excel Excel via formulas
=C3/2
=D3+C4
=D4*55000
show: out of 55000 for 7 steps covered 54570
numbers in their sequences
and probably deviation betrays a false accident
and shuffling involved 54885 close to theory
Theoretical values in Excel Excel via formulas
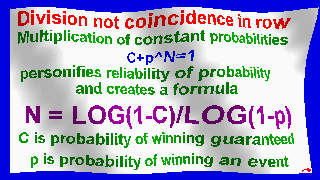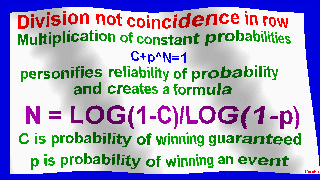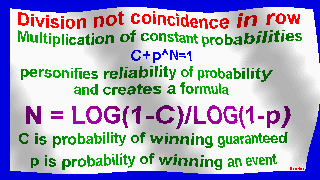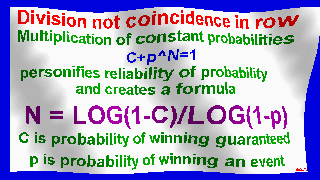





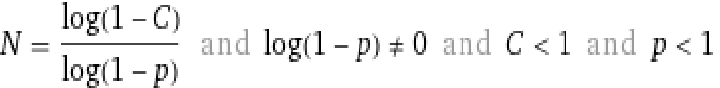
Comment